Investissement crypto : c'est quoi les intérêts composés (compound) ?

Tout le monde connait le principe des intérêts. Que ce soit via un prêt, ou via de l’investissement, le fait d’obtenir un rendement pour ses actifs est quelque chose de classique. Mais est-il possible de faire mieux que de simples intérêts ? Qu’est-ce qu’un intérêt composé ? Voyons tout cela ensemble !

Un intérêt, c’est quoi ?

Avant d’aller plus loin, nous devons redéfinir ensemble ce que sont les intérêts. Qu’ils soient liés à un prêt (bancaire par exemple) ou à un rendement d’épargne, le principe est le même.

Attention, quelques notions mathématiques de base sont nécessaires pour comprendre le fonctionnement, notamment sur les intérêts composés.

Voyons comment ça fonctionne de manière simple avec un exemple.

Imaginons que j’investisse 1000€ à un taux d’intérêt de 5% par an, pendant 3 ans.

La formule de calcul à appliquer est simple :
In = les intérêts gagnés
C = mon capital de départ (ici 1000€)
R = le taux d’intérêt (ici 5%) que l’on écrira sous la forme 0,05
T = la durée de mon investissement, en année (ici 3).

La formule donne In = C x R X T

Nous aurons donc sur une année In = 1000 x 0,05. In vaudra donc 50€.

Après 3 ans, nous aurons accumulé 50 x T = 50 x 3 = 150€

C’est le fonctionnement d’un intérêt simple.

Un intérêt composé alors, ça marche comment ?

Avec les intérêts composés, le calcul est un peu différent, car nous allons tenir compte, en plus du capital de départ, des intérêts accumulés sur les périodes précédentes.

Le but étant d’obtenir ce que l’on pourrait appeler un effet « boule de neige ».

La formule à utiliser est désormais la suivante :

In = le montant final (capital de départ + intérêts)
C = capital initial de 1000€
R = le taux d’intérêt annuel, toujours de 5%, écrit sous la forme 0,05.
N = le nombre de fois que mes intérêts sont capitalisés, par an. Ici nous prendrons 1, car le calcul ne se fera qu’en fin d’année.
T = la durée en année (toujours 3)

La formule finale est donc In=C×(1+R/N​) ^NT

La première année, pas de changement. J’investis 1000€, au bout d’un an j’ai 1050€ sur mon épargne.

La deuxième année, le calcul tiendra compte de la plus-value générée.
1050 x (1 + 0,05) = 1102, 50€
On peut voir que j’ai gagné 2,50€ de plus qu’avec un fonctionnement d’intérêt simple.

La troisième année nous aurons ceci :

1102,50 x (1 + 0,05) = 1157,63€

Après 3 ans, mon capital est donc de 1157,63€, soit 7,3€ de plus que pour un calcul avec intérêt simple.

Quels facteurs influent sur mon rendement ?

Comme nous pouvons le voir avec la formule, trois choses influent grandement sur le gain que vous allez avoir à la fin de votre période d’épargne.

• Le rendement annuel.
• La fréquence d’applications des intérêts (appelée fréquence de capitalisation). Plus elle sera courte, plus les gains seront importants, car l’effet « boule de neige » sera amplifié. Une fréquence journalière est plus avantageuse qu’une fréquence trimestrielle.
• La durée d’investissement. Plus la durée est longue, plus l’effet est fort.

Il est donc important de garder en tête qu’un gain « conséquent » avec des intérêts composés nécessitera forcément du temps. Sur une épargne très courte, la différence ne sera quasiment pas visible avec une épargne classique.

Le montant investi est forcément un levier puissant également. Plus la somme de départ est importante, plus l’effet « boule de neige » sera impactant.

Maintenant, imaginons que, comme il l’est souvent proposé sur les plateformes de staking / épargnes cryptos, les intérêts annuels soient « mensualisés ». Autrement dit, le taux de 5% par an est appliqué et calculé tous les mois.

Si on reprend notre formule In=C×(1+R/N​) ^NT , nous avons donc maintenant N = 12, et T vaut toujours 3. La formule devient donc In = 1000 x (1+ 0,05 / 12) ^12×3

0,05/12 donne 0,0041667 (arrondissons). Ajoutés à 1, nous avons une valeur de 1,0041667, c’est la partie du calcul qui est dans la parenthèse.
Si on élève cette valeur à la puissance de ^NT qui vaut 12 x 3, on obtient 1,0041667 ³⁶ ce qui donne environs 1,1612.

Multiplions cette valeur par le montant de notre capital initial de 1000€ et on obtient environ 1161,20€.

Soit un capital final de 1161,20€. Cela représente 3,57€ de plus qu’avec les intérêts composés annuels, et 12,20€ de plus qu’avec les intérêts simples.

Exemple avec de la cryptomonnaie

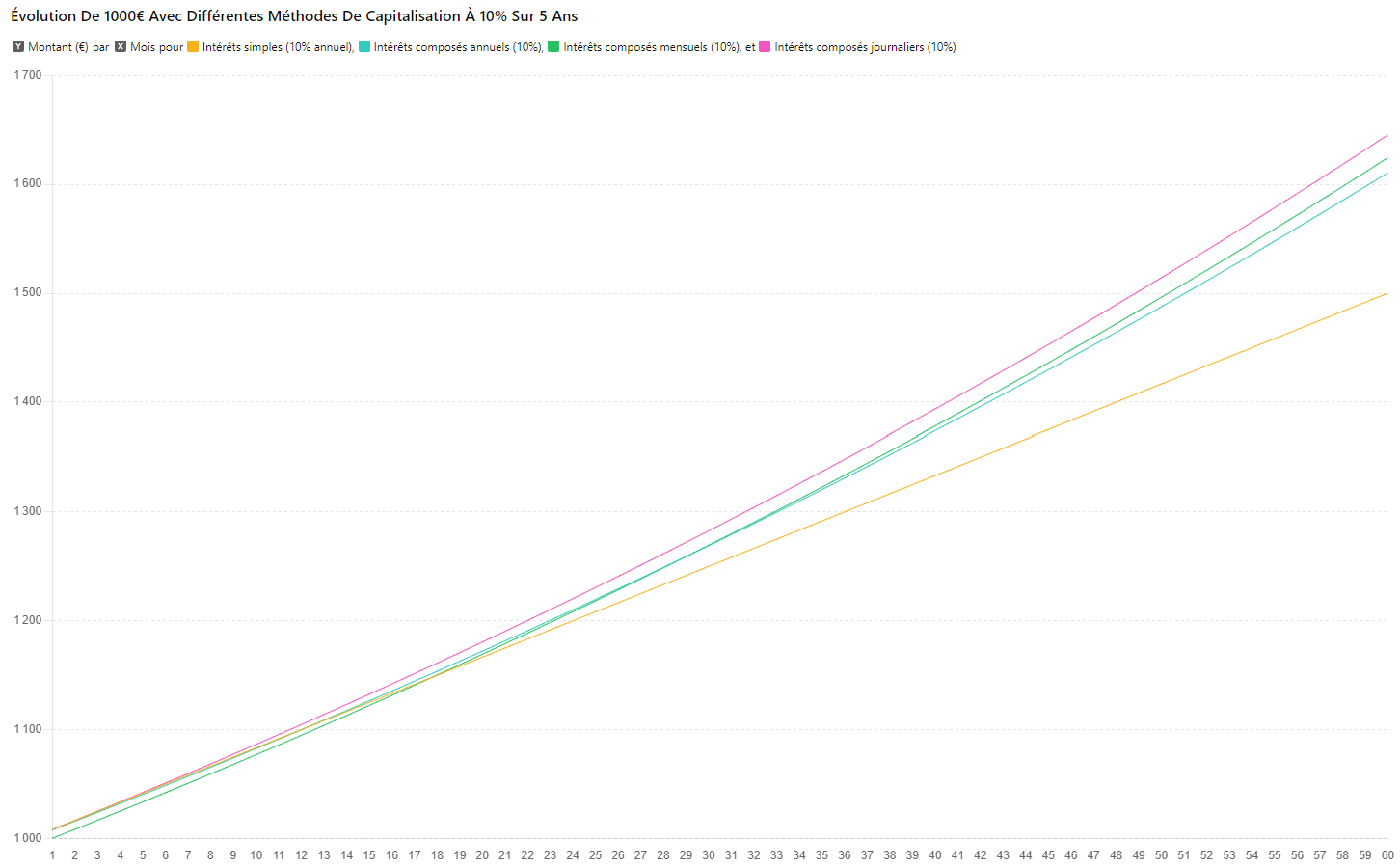
Maintenant, imaginons que l’on souhaite placer 1000$ en USDT sur un rendement DéFi de 10%. Comparons le résultat de cet investissement, avec les intérêts simple, composés annuellement, composés mensuellement et composés journalisés pendant 5 ans.

Et si on couplait tout ça avec du DCA ?

Si vous n’êtes pas à l’aise avec le concept de DCA, prenez le temps de lire cet article.

C’est fait ? Ok ! Maintenant, regardons ensemble ce que peuvent donner des intérêts composés, avec un DCA en supplément.

Imaginons que le capital de départ est de 1000€ et que chaque mois, nous investissons 100€ de plus via le DCA, qui viennent s’ajouter à l’épargne.

Le taux d’intérêt est de 10% par an, distribué mensuellement. Quel serait le résultat après 3 ans de placement ?

Nous avons investi 1000€ + (100€ x 36) soit 4600€. Au bout de 3 ans, notre capital s’élève alors à 5561,18€ soit un gain net de 961€.

Avec un versement sur un compte classique, à 10% d’intérêt par an, nous aurions « seulement » 4900€ au bout des ces 3 ans, soit une différence de 661,18€

Vous avez saisi le principe de fonctionnement ? C’est passionnant non ?

Je vous propose de nous arrêter ici pour cet article, qui avait pour but de vous présenter le fonctionnement, et les calculs. Nous nous retrouverons bientôt pour vous présenter les outils existants pour vous faciliter la tâche dans ces calculs, afin d’optimiser au mieux vos rendements, et faire un point sur les risques et les points à ne pas négliger (frais cachés par exemple). À très bientôt !